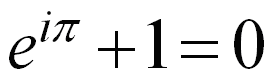Tutti noi abbiamo nella nostra memoria giornate che, senza annoverare avvenimenti eccezionali, si stampano nella nostra mente per sempre, e tornano di tanto in tanto. Questa che racconto adesso risale a trent’anni fa, eppure è sempre lì, e chissà perché in questo periodo mi capita di tornarci coi pensieri.
Ero con la famiglia a Newport, Oregon. Ne venivamo da due anni in California, eravamo tornati lì altri tre mesi dopo un anno di rientro, e il viaggio nel Nord della California e in Oregon rappresentava la vacanza conclusiva. Passando dal porto, ho visto un negozietto dove affittavano la “cage” per la pesca dei granchi, con annesso tutto l’occorrente. Subito dopo il pranzo in campeggio, parto coi due figli grandi, Andrea di 9 anni e mezzo ed Emanuele di 4, per provare questo tipo di pesca. Ci forniscono di tutto l’occorrente, compreso un pezzo di pesce surgelato come esca e lo strumento per misurare la lunghezza dei granchi catturati. Le leggi lì sono molto severe, si possono prendere solo quelli di un certi tipo, solo i maschi, e solo se raggiungono una certa lunghezza. Partiamo, andiamo sul molo, e cominciamo le operazioni. In acqua non si vede nulla, non ci sono segni se i gamberi arrivano o no, bisogna tirare su la gabbia ogni tanto. Per mezzora non succede nulla, non vediamo nemmeno un granchio, cominciamo a essere un po’ frustrati. Si avvicina una persona anziana con la moglie, inizia a parlare con Andrea, che ovviamente manovra la gabbia. Io capisco solo “Vietnam veteran”, ma Andrea apparentemente capisce, perché mi spiega che ci sono le foche che mangiano i granchi, e che bisogna essere più rapidi a tirare su (io ovviamente gli dicevo di avere pazienza). E, miracolo, cominciamo a vedere granchi! Dopo un po’ il veterano se ne va, e arriva qualche turista. Andrea acconsente a lasciar provare me, perché decide che per lui è più divertente fare l’esperto pescatore di granchi, e spiegare ai turisti come si pescano, che si deve fare e perché, e quanto siano dispettose le foche. Io intanto ogni tot tiro su la gabbia, dalla quale escono spesso granchi che corrono qui e là. Si credono di riuscire a scappare, ma c’è Emanuele, che ha imparato dal veterano come si prendono in mano, che li cattura velocissimo e poi ne lancia la maggior parte in acqua, dicendo, alternativamente: It’s a girl! Too short! Wrong type! Siamo andati avanti almeno un paio d’ore, accompagnati da un rumore continuo come di tuono. Stava facendo quasi buio, quando riportiamo la gabbia e lo strumento misuratore al negozio, e decidiamo di provare a seguire il suono per cercare di capire che cosa lo causasse: arriviamo a una spiaggia letteralmente coperta da leoni di mare, che evidentemente conversavano. Rientriamo in campeggio, e mi dico che no, non è stato un sogno stravagante, ma solo una giornata davvero particolare.
Stamattina mi sono svegliato con in testa il concetto di fake news in matematica. Ho deciso di riflettere sull’idea se anche in matematica esistono fake news, magari molto radicate e quindi difficili da smontare, e sono arrivato alla conclusione che a mia conoscenza ce ne sono almeno due. Le descrivo brevemente.
La prima.
Consideriamo una somma infinita come questa:
1-(1/2)+(1/3)-(1/4)+…
C’è un accordo generale sul fatto che questa addizione di infiniti termini abbia un risultato finito, pare lo garantisca uno di una certa importanza, di nome Leibniz, e qualcuno arriva a dire che sa benissimo quanto vale quella somma, qualcosa tipo ln 2.
E fino a qui nessun problema. Questi nascono per il fatto che qualcuno afferma che se io comincio a scambiare tra loro un po’ di addendi, cioè magari comincio a fare
1+(1/3)-(1/2)-(1/4)+…
allora potrebbe venire un risultato diverso! Ma si sa che nel tempo le fake si perfezionano, e questa ora ha assunto la seguente grottesca formulazione:
Prendi una serie qualsiasi, come quella di sopra, che ha caratteristica di convergere, ma che è infinita se invece di alternare i segni li prendi tutti col segno più (si sa che 1+(1/2)+(1/3)+(1/4)+… fa proprio più infinito), fissa un qualunque numero reale, o anche +infinito e mettici pure meno infinito, e chiamalo a; allora esiste un modo di riordinare (cioè cambiare l’ordine degli addendi) della somma in modo che il risultato finale sia a.
Beh, è stupefacente che ci sia gente che crede a una balla simile.
La seconda fake, a parole si può dare così (dopo una formulazione più matematica)
Prendo il quadrato [0,1]x[0,1], e a ogni suo punto associo o il valore 0 o il valore 1. Con il vincolo seguente: se fisso un segmento verticale qualsiasi del quadrato, gli 0 devono essere pochi, la misura dei punti dove metto 1 deve essere 1, cioè la misura di tutto il segmento. Dopo aver fatto questa operazione, vi sfido a tracciare una linea continua (che sia un grafico) dentro il quadrato e a passare in almeno un punto dove ci sia un 1. Ovviamente ci provate con aria di sufficienza, gli 0 sono talmente pochi… ma il vostro primo tentativo va a vuoto. Ok, pensate, avete avuto una botta di sfiga, ci provate riprovate, ma niente da fare! Proprio non ci riuscite, accidenti!
Si possono affermare cose più ridicole?
Adesso la stessa fake col formalismo matematico.
Esiste una funzione f(x,y) definita nel quadrato [0,1]x[0,1], e con le proprietà seguenti:
1) per ogni fissato x, f(x,y)=0 su un insieme al più numerabile;
2) f(x,y(x))=0 per ogni y(x) da [0,1] in [0,1] e continua.
Si può affermare cose più ridicole?
Naturalmente, dietro a queste storielle, che possono venire in mente solo a un matematico in quarantena (e senza ragazzini in casa), ci sta sempre una morale, ma di questa ne parliamo tra qualche giorno…
E’ notizia di stanotte che è morto John H. Conway, matematico davvero geniale. I suoi contributi sono stati fondamentali in molti campi. Un gioiello tra i suoi risultati è una teoria di tipo assiomatico, che riguarda certi tipi di giochi.
Tempo fa ho scritto con l’amico Rosolini e pubblicato con Franco Angeli un libretto, Matematica al bar. Nel capitolo quinto si dialoga, sottolineo al bar, di questa teoria di Conway.
Qui lascio il link al nostro capitolo, se qualcuno vuol dare un’occhiata.
Nel nostro dialogo citiamo anche un libretto di Knuth, Numeri surreali, che parla di questa teoria in forma di racconto, e diciamo una cosa che era vera allora, ma non lo è oggi: che purtroppo questo delizioso libretto non è stato tradotto in Italiano. Oggi la traduzione è disponibile (fatta da un altro amico, Francesco Oliveri) e pubblicato da Franco Angeli https://www.francoangeli.it/Ricerca/scheda_libro.aspx?id=23192.
Può capitare di essere un week end di Maggio a Cesenatico, e di vedere in una cittadina altrimenti poco frequentata, data la stagione, girare per le strade tanti ragazzi e ragazze. Non è questa la cosa strana, strano è quel che senti, se qualcuno parla a voce più alta del solito: a me veniva due alla a meno uno più due alla b -1=5…non sono certo i discorsi che ti aspetti sentire in una località di mare da ragazzi a passeggio! Che succede allora a Cesenatico un certo week end di Maggio? Succede che un grande numero di ragazzi si reca lì, accompagnati dai loro professori, per le finali delle Olimpiadi di matematica. E’ un evento interessante e molto importante, ci sono molte persone coinvolte e che lavorano, volontariamente, alla riuscita di questa manifestazione. Gli eventi a Cesenatico sono la conclusione di un lungo processo di selezione, processo che si sviluppa in tutta Italia, coinvolgendo un numero sorprendente di ragazzi e delle loro famiglie. Sono utili queste Olimpiadi della matematica: al di là del fatto che due tra i più famosi matematici italiani odierni (uno è Figalli, medaglia Fields, l’altro De Lellis, che ha una posizione Princeton, IAS) mi hanno detto esplicitamente che fare bene alle Olimpiadi è stato per loro il primo passo nella decisione di diventare matematici di professione, l’esperienza che fanno tanti ragazzi è certamente molto formativa. A me piace particolarmente l’idea della gara a squadre. La scuola di ogni ordine e grado non incentiva, di solito, il lavoro di equipe, ma questo è quel che la maggioranza delle persone fa quando va a lavorare, e quindi questo lavoro in team è un esperienza preziosa…
Quest’anno l’Unione Matematica Italiana mi ha fatto l’onore di chiedermi di tenere una conferenza per gli insegnanti (mentre gli alunni erano in gara), molto in tema visto che mi invitano a parlare di giochi.
Ho promesso ai presenti che avrei messo sul sito le slides della mia presentazione: lo faccio ora, con consueto ritardo.
 Pensare ingenuo, pensare strategico
Pensare ingenuo, pensare strategico
La teoria dei giochi vuole affrontare lo studio di problemi che coinvolgono più persone da un punto di vista strategico. Ora strategico è anche una bella parola, ma occorre riempirla di significato, altrimenti si fa retorica… Per questo chiarisco l’affermazione precedente, attraverso un esempio semplice, anche per mostrare come la teoria ci permetta di tirare spesso conclusioni ovvie, ma inaspettate prima di fare un’analisi della situazione. Del resto questa è una delle caratteristiche principali della teoria dei giochi: proporre soluzioni che ci paiono ovvie, ma solo dopo che ci sono state proposte. Ecco dunque l’esempio. Sono in aula, e propongo ai mei tre (quel che importa è che siano dispari, per evitare possibili pareggi, qui scrivo tre per semplificare le cose, di solito ne ho molti di più!) alunni di scegliere tra le due opzioni: un compito molto facile, o un altro fattibile ma assai più difficile. Avete capito subito che chi studia giochi ama mettere le persone in imbarazzo… i miei tre allievi sanno che se chiedono il compito difficile ci guadagnano in reputazione, ma nello stesso tempo un compito più facile è una tentazione irresistibile. E dunque che fare? Visto che chiederò a ognuno di loro di dire pubblicamente e in sequenza che cosa propongono, sarà più conveniente essere il primo interpellato, oppure l’ultimo? E come andrà a finire? L’intuizione ci dice che alla fine darò loro il compito più facile, ma che cosa sperare, essere chiamati per primo, per secondo o per terzo? E’ un test che mi diverto a fare spesso, e che in genere dà lo stesso risultato: la maggioranza vorrebbe essere l’ultimo a votare, qualcuno, molto pochi, vorrebbe essere il secondo, altri il primo. Questo gioco si può facilmente analizzare costruendo il suo albero, e questo ci servirà a capire come generalizzare il ragionamento per portarlo a situazioni più complesse, ma qui possiamo capire la risposta basandoci su un semplice ragionamento. Lasciando perdere chi vorrebbe essere il secondo a votare-chi sceglie questa opzione si basa esclusivamente su qualche suggestione psicologica- e proviamo a immaginare su che ragionamento si basa chi vorrebbe decidere per ultimo. Io credo che sia questo: dal momento che so che i miei compagni, come me, non hanno nessuna voglia di affrontare un compito difficile, meglio che votino prima loro. Voteranno per il compito facile, al mio turno questa opzione ha la maggioranza, quindi io posso votare quel che voglio, e quindi posso fare la mia bella figura!
Perché è sbagliato questo ragionamento, che ho visto fare persino in occasioni di certe delicate decisioni accademiche (voto per ultimo perché a quel punto i giochi saranno fatti, quindi non sono costretto a votare quel che voglio, ma posso votare quel che voglio che gli altri credano sia la mia scelta preferita)?
Perché si può rovesciare completamente! Che succede infatti se il primo annuncia che sceglie il compito più difficile? Succede che gli altri due sono costretti a votare per il compito più facile, perché tra le due alternative non c’è paragone su quel che preferiscono fare… Dunque il primo forza gli altri a fare una scelta, ottenendo così il massimo risultato possibile per sé.
Questo ragionamento si può generalizzare. Ogni volta che un certo numero di persone devono prendere decisioni in sequenza, almeno teoricamente si può procedere andando a vedere come si comporteranno i giocatori che devono prendere la decisione finale. Questa informazione è utile per i giocatori che devono prendere una decisione subito prima di quelli che prendono la decisione finale… e così via. Si chiama metodo di induzione a ritroso. Questo metodo ci insegna che, molto spesso, nei giochi è meglio essere il primo a muovere. Molto spesso ovviamente non vuol dire sempre…ad esempio nessuno vorrebbe essere il primo a giocare a sasso carta forbici! Ma ad esempio nel gioco chiamato del Nim, che consiste nell’avere un certo numero di mucchietti di carte sul tavolo, e i due giocatori a turno tolgono un certo numero di carte dallo stesso mucchietto, e che pulisce il tavolo vince, ebbene mettendo un numero a caso di mucchietti ciascuno con un numero a caso di carte, la probabilità che il primo vinca è molto alta: nel caso di due mucchietti, il secondo vince solo se i due mucchietti hanno lo stesso numero di carte.
«Non si tratta di scegliere quei volti che, giudicati obiettivamente, sono realmente i più graziosi, e nemmeno quelli che una genuina opinione media ritenga i più graziosi. Abbiamo raggiunto il terzo grado, nel quale la nostra intelligenza è rivolta ad indovinare come l’opinione media immagina che sia fatta l’opinione media medesima. E credo che vi siano alcuni i quali praticano il quarto, il quinto grado e oltre» .
Chi scrive queste parole è l’economista J.M. Keynes, uno dei più influenti del secolo scorso, il riferimento principale per chi oggi non ama le politiche del rigore. Keynes, detto per inciso, non ha vinto il premio Nobel per l’Economia, ma ha avuto importanti onorificenze, quali quella Baronetto della Corona Britannica e Barone Keynes di Tilton, Ufficiale dell’ordine di Leopoldo (un’onorificenza belga), ma soprattutto quella di Compagno dell’Ordine del Bagno, che non sarà il Nobel, ma a me sembra davvero bellissima, e probabilmente è molto prestigiosa… Ma a parte questo folklore, a che cosa si riferisce Keynes, con le parole di sopra, e perché sono interessanti per la teoria dei giochi? Si riferisce a un immaginario concorso di bellezza, in cui i votanti riceveranno un piccolo premio se riescono a indovinare chi sarà la donna più votata. Keynes osserva che l’approccio più ingenuo porterebbe a votare quella che ci piace di più, ma che per vincere non bisogna comportarsi così: ed ecco che oggi, come lui osserva, si è arrivati a un terzo livello di pensiero, per cui “la nostra intelligenza è rivolta ad indovinare come l’opinione media immagina che sia fatta l’opinione media medesima”.
In teoria dei giochi assumiamo, almeno quando poniamo i suoi fondamenti, che i giocatori non abbiano nessun limite al livello di pensiero cui possono arrivare: eccone un esempio tanto semplice quanto carino. Che sia carino me lo dimostra il fatto che lo faccio spesso con i ragazzi delle scuole e loro si divertono moltissimo a farlo, soprattutto quelli che vincono.
Il gioco è il seguente: invito tutti i presenti a scrivere il loro nome e cognome su un foglio, oltre a un numero compreso tra 1 e 100. Poi ritiro tutti i foglietti e faccio calcolare da qualcuno la media dei numeri ottenuti; se i presenti non sono molti, con un telefonino a disposizione ottengo una risposta in meno di 5 minuti.
Ora si tratta di stabilire chi vince (o i vincitori, possono essere più di uno). Bene, detta M la media calcolata precedente, vince chi si avvicina maggiormente alla metà di M.
Dunque, che scrivereste voi sul vostro foglietto, e che cosa scrive il teorico dei giochi? Io non posso sapere che cosa scrivereste voi, ma posso spiegarvi che cosa scrive il teorico dei giochi, che certamente non vince, ma avrà almeno la soddisfazione di scrivere la risposta giusta. Ricordiamoci che il teorico dei giochi sa di essere una persona perfettamente razionale, ed assume che anche gli altri lo siano.
Ecco allora il ragionamento:
Primo livello di pensiero:
M ovviamente non può essere maggiore di 100, visto che a nessuno è concesso di scrivere un numero maggiore. Dovendo cercare di avvicinarmi alla metà di M, dunque non ha senso scrivere un numero maggiore di 0,5 x 100= 50.
Secondo livello di pensiero:
questo ragionamento viene fatto da tutti i giocatori, per cui nessuno scrive un numero maggiore di 50. Allora in effetti M non può essere maggiore di 50. Dovendo cercare di avvicinarmi alla metà di M, dunque non ha senso scrivere un numero maggiore di 0,5 x (0,5×100) = (0,5)2 x 100= 25
…
Ennesimo livello di pensiero:
questo ragionamento viene fatto da tutti i giocatori, per cui nessuno scrive un numero maggiore del numero k trovato al livello (n-1). Allora in effetti M non può essere maggiore di 0,5 k. Dovendo cercare di avvicinarmi alla metà di M, dunque non ha senso scrivere un numero maggiore di 0,5 x (0,5 k) che con un conto molto semplice si vede essere (0,5)n x 100
Ricordandoci che questo ragionamento siamo in grado di farlo per ogni numero naturale n, e ricordando che (0,5)n diventa sempre più vicino a zero (in termini pomposi si dice che tende a zero quando n tende a più infinito), la risposta inesorabile è quindi che dovremmo scrivere tutti 1, il più piccolo numero che ci è concesso scrivere.
Naturalmente chi scrive 1 può scordarsi di vincere. Una piccola ma interessante osservazione è che ho scelto la regola di avvicinarsi alla metà di M, ma si arriverebbe allo stesso risultato anche se avessi scelto di avvicinarsi a 0,9 M, o anche a 0,99 M. Eppure potete scommetterci che se proponete di moltiplicare M per un numero molto vicino a 1, le risposte medie delle persone saranno ben più grandi di quelle che avrete chiedendo di moltiplicare M per un numero molto vicino a 0.
(La citazione è presa da J.M. Keynes, General Theory of Employment, Interest and Money, Palgrave Macmillan, London 1936; trad.it. Teoria generale dell’occupazione, dell’interesse e della moneta, a cura di T. Cozzi, Utet, Torino 2006, p. 342).
Che fare se si presentano gli alieni a casa nostra?
Un giorno una rivista ha chiesto a me e ad altri di scrivere 20 righe sul tema: che fare se si presentano gli alieni a casa nostra? Io avevo risposto in questo modo.
 Gli alieni si presentano a casa nostra. Che fare? E soprattutto che cosa NON fare? Partiamo da una premessa. Si è verificato un avvenimento che aveva probabilità molto piccola! Questo succede più sovente di quel che immaginiamo, ma in genere le situazioni che tali avvenimenti improbabili ci propongono sono inusuali, e quindi richiedono di riflettere. Quindi l’unica cosa veramente indispensabile da fare è: non dare nulla per scontato. È chiaro che saremo di fronte a esseri super intelligenti, perché non c’è dubbio che arrivano da lontano, e dunque sono stati in grado di fare un viaggio lunghissimo. Siccome ci crediamo anche noi intelligenti, potremmo aspettarci che capiscano i nostri discorsi. Nulla di più sbagliato! Un grande pensatore ci ha insegnato che neppure una cosa semplice come l’aritmetica può certificare la sua completezza e la sua coerenza, figurarsi il nostro pensiero! Non solo, ma l’idea di infinito, che oggi ci è necessaria per una comprensione più profonda delle cose, ha distrutto la comoda credenza che la logica, la semplice logica, sia un linguaggio universale e necessariamente unico. Oggi, sappiamo che si possono utilizzare molteplici logiche, che a volte dicono cose assai diverse…e se le nostre menti intelligenti ma limitate sono capaci di immaginare molte logiche possibili, quanti saranno i modi per esprimersi intelligentemente? Davvero così tanti da non poterli neppure immaginare. Per questo, la nostra intelligenza e quella dell’alieno saranno così diverse da non riuscire a capirsi, almeno all’inizio. Solo se non daremo nulla per scontato avremo una possibilità di dialogo.
Gli alieni si presentano a casa nostra. Che fare? E soprattutto che cosa NON fare? Partiamo da una premessa. Si è verificato un avvenimento che aveva probabilità molto piccola! Questo succede più sovente di quel che immaginiamo, ma in genere le situazioni che tali avvenimenti improbabili ci propongono sono inusuali, e quindi richiedono di riflettere. Quindi l’unica cosa veramente indispensabile da fare è: non dare nulla per scontato. È chiaro che saremo di fronte a esseri super intelligenti, perché non c’è dubbio che arrivano da lontano, e dunque sono stati in grado di fare un viaggio lunghissimo. Siccome ci crediamo anche noi intelligenti, potremmo aspettarci che capiscano i nostri discorsi. Nulla di più sbagliato! Un grande pensatore ci ha insegnato che neppure una cosa semplice come l’aritmetica può certificare la sua completezza e la sua coerenza, figurarsi il nostro pensiero! Non solo, ma l’idea di infinito, che oggi ci è necessaria per una comprensione più profonda delle cose, ha distrutto la comoda credenza che la logica, la semplice logica, sia un linguaggio universale e necessariamente unico. Oggi, sappiamo che si possono utilizzare molteplici logiche, che a volte dicono cose assai diverse…e se le nostre menti intelligenti ma limitate sono capaci di immaginare molte logiche possibili, quanti saranno i modi per esprimersi intelligentemente? Davvero così tanti da non poterli neppure immaginare. Per questo, la nostra intelligenza e quella dell’alieno saranno così diverse da non riuscire a capirsi, almeno all’inizio. Solo se non daremo nulla per scontato avremo una possibilità di dialogo.
Qualche anno fa ho pubblicato un libro pensato e scritto assieme a un amico, Pino Rosolini. Si chiama Matematica al bar. Si parla molto di matematica, ma anche di altro. C’è un pezzo dedicato al talento, in cui mi sono divertito a parlare dei miei idoli sportivi (lui ha parlato meno, è meno appassionato di me di sport). Siccome si parla anche un po’ di Federica Pellegrini, ho chiesto a Pino di estrarre dal libro il capitolo sul talento, come piccolo omaggio all’impresa di Federica di ieri.
MatematicaAlBar_MatematicaSportTalento
Aggiungo oggi, 28 Febbraio 2018, che nel frattempo Roger è tornato numero uno. Per la classifica ATP. Perché per il tennis e chi lo ama, lui è sempre il numero uno.
Su Facebook, strumento peraltro benedetto per molti motivi, i dibattiti, anche tra persone di garbo e di cultura, spesso si riducono a posizioni contrapposte e inconciliabili. Però ci sono argomenti troppo importanti per liquidarli in due battute, o per rischiare di arrabbiarsi con persone che si stimano, perché due battute raramente riflettono la complessità della situazione. L’ultima faccenda che ha sollevato la mia attenzione è quella della ragazza rumena che ha messo dei post su Facebook e per questo si è vista revocare la libertà provvisoria. Questo episodio ha scatenato reazioni, in un senso o nell’altro, direi sempre del tipo o bianco o nero. Non è così. La realtà è complessa, e mai di un colore solo. Allora ci ho pensato un po’ su, e queste sono le mie considerazioni. Che rivolgo soprattutto a quelli che hanno dimostrato molta umana comprensione per la ragazza, con gli altri credo che il confronto sia sostanzialmente inutile, quindi mi interessa poco (ma non è detto, se qualcuno argomenta bene…)
Una delle cose più importanti, secondo me, del buon ragionare è non confondere gli argomenti. Dire cose giuste ma che c’entrano poco con l’argomento in questione secondo me non rafforza gli argomenti…anzi. Allora mi pare che si sia fatta una grande confusione, mettendo assieme tre cose diverse:
- L’entità della pena
- Il regime di semilibertà
- Il comportamento della ragazza durante questo regime.
E’ l’ultimo punto quello cruciale, ma chiarisco un secondo anche la mia opinione sui primi due.
Il primo. Non mi sento in grado di dire, nella maniera più assoluta, se tot anni sono pochi o tanti per una certa condanna. Rilevo solo che alla ragazza sono stati dati due anni in meno del massimo previsto per il delitto da lei commesso. A ragionare terra a terra, mi sembra una sentenza ragionevole. Sarà stato un omicidio preterintenzionale, ma sicuramente le circostanze sono molto aggravanti. Un conto è spingere una persona, un conto è usare un ombrello come una spada ad altezza viso.
Il secondo. Io capisco che si possa anche essere in disaccordo, ma ritengo una conquista di grande civiltà, in ben precise circostanze, usare un atteggiamento intelligente e comprensivo per recuperare le persone. Sia chiaro. Per me è una sciocchezza bella e buona sostenere che il carcere serve per rieducare una persona, o cose simili. Il carcere è, prima di tutto, una forma di difesa della società nei riguardi di chi infrange le sue regole. Se così non fosse, la legge del taglione sarebbe più semplice, diretta, economica. Invece chi ammazza sulla metro colpisce anche me (o anche chi ruba, non paga le tasse, fa falsi in bilancio, sia ben chiaro), perché viola le regole del comportamento che ci siamo dati. Quindi prima di tutto la pena è una punizione, a garanzia di tutti. Però collaborare è un sistema efficiente, per gli individui e per la specie, e quindi ogni volta che si può fare qualcosa per qualcuno che ha sbagliato, trovo che sia nobile, importante, nonché utile, efficiente farlo. Quindi, anche se emotivamente (non ho né prove né statistiche rigorose) ho l’impressione che licenze premio, regimi di semilibertà ecc ecc siano in genere concessi con un po’ di leggerezza, io sono del tutto favorevole a che la pena nel tempo possa evolvere in forme sempre meno costrittive per rendere il meno difficile possibile il reinserimento della persona colpevole nella comunità.
Però non va dimenticato che una persona in questo regime diverso dalla detenzione pura e semplice sta sempre scontando una condanna. Se una persona è condannata a 16 anni, questa è la sua pena. Per me, per noi essa sarà libera, avrà saldato il suo debito, al termine della pena, non prima (in alcune circostanze ammetto che si possa anche decidere che la pena si estingue in anticipo, ma deve essere una decisone ben chiara e soprattutto eccezionale ed eccezionalmente motivata). Prima, se qualcuno con senso di responsabilità vuol decidere che la persona può passare del tempo fuori dal carcere, può stare con i figli, io sono favorevole. Ma questa persona non è una persona libera. Per cui io non credo che ad essa vadano negate piccole grandi gioie della vita, ma sempre tenendo conto dello stato di persona che sconta una pena. Una tale persona non può essere attiva sui social, non deve andare in tv a farsi intervistare, deve “vivere nascosta” (λάθε βιώσας).
Dopo di che, vorrei aggiungere perché sia ben chiaro, ritengo la ragazza la meno colpevole di tutti di questa situazione; io non posso aspettarmi che una persona con una storia così difficile sia in grado di distinguere con chiarezza quel che può e non può fare: il giudice e il suo avvocato però sì.
Il nostro cervello, quando lo usiamo bene, fa cose bellissime. Per esempio, si accorge che possiamo individuare tanti insiemi di numeri. Il primo è quello dei numeri naturali: 0,1,2,3,… Sono quelli che ci sembrano i più amichevoli, i meno spaventosi, anche se in verità anche loro nascondono talvolta insidie terribili. Però persino gli animali, pare, hanno innato il senso del numero, e noi nasciamo con i numeri dall’1 al 4 (pare, da studi recenti) già codificati nel nostro cervello. Ma certo, nella nostra divorante curiosità, non possiamo accontentarci, ed ecco che ci si presenta alla mente l’insieme dei numeri interi, che comprende i naturali, ma ci aggiunge anche i numeri negativi: una bella astrazione davvero; in natura, fisicamente intendo, non è facile spiegarli, però li possiamo capire abbastanza presto: Matteo, 6 anni, l’altro giorno mi spiegava che prima di 0 ci sono -1,-2,-3,… Mica ci fermiamo qui! Siamo in grado di immaginare anche numeri sotto forma di frazioni. Ci viene molto comodo pensare a 2/3 come un numero, e gli diamo anche un nome importante: numero razionale, non perché sappia fare ragionamenti complicati, ma per un fatto etimologico, razionale da ratio, cioè rapporto: 2/3 è un numero rapporto di due numeri. Ci basta l’insieme dei numeri razionali? O la nostra voglia di capire ci porta a immaginare altri numeri? La risposta è scontata, e ci viene, secondo la leggenda, da Pitagora: certo che no! , il numero radice(2), che rappresenta una cosa concreta (il che ovviamente non è vero, ma se lo diciamo nessuno ce lo contesta…) perché è la lunghezza della diagonale del quadrato di lato unitario, non può essere scritto come rapporto di due numeri interi. Per questo lo chiameremo, come tutti quelli come lui, numero irrazionale: è irrazionale perché non è esprimibile come rapporto. Tra l’altro, piccolo inciso, visto che stiamo parlando di insiemi infiniti, ci potrebbe venire la voglia di porci domande del tipo: ma i numeri razionali sono di più di quelli naturali? Attenti a rispondere! Proprio perché parliamo di insiemi infiniti, occorre definire correttamente che cosa vuol dire che due insiemi hanno lo stesso numero di elementi, o uno ne ha di più di un altro. Comunque, la risposta è no! Tutti i numeri che si possono esprimere come frazioni sono tanti quanti i naturali….la cosa sconvolgente è che invece i numeri reali, che comprendono razionali e irrazionali, sono di più! Se chiedete a uno studente dei primi anni di una facoltà scientifica di elencare un po’ di numeri irrazionali, dopo aver detto, in un crescendo di agitazione, radice(2), pigreco e e, si sconforta perché non gliene vengono in mente altri, è un fatto che i numeri irrazionali sono appunto ben di più di quelli che si possono descrivere come frazioni.
Ovviamente la storia mica finisce qui. Mica possiamo accontentarci dei numeri reali, cioè dei razionali e degli irrazionali. Una buona ragione per essere insoddisfatti è che qualunque sia il numero reale r, se ne prendete il suo quadrato, r2, questo è un numero positivo. E per forza mi direte, rappresenta l’area del quadrato di lato r, quindi deve essere un numero positivo! Tutto vero, ma questo ci limita, perché siccome ci piace che le equazioni abbiano soluzione, come la mettiamo con l’equazione x2+1=0? Beh, mica è complicato! Basta immaginare un nuovo insieme di numeri, dove questa equazione ha soluzione! Ecco che nasce l’insieme dei numeri complessi, che ai reali aggiunge quelli immaginari, appunto (e li fa operare assieme).
Ma siccome la matematica va presa a dosi piccolissime, per il momento arriviamo a una conclusione, sempre provvisoria, ovviamente…è imperativo diffidare di chi vi dice, in qualunque campo, che si è arrivati alla conclusioni definitive…
La conclusione cui vorrei arrivare è che certe questioni vanno inquadrate nel contesto, e nell’insieme, corretti. Prendiamo la fatidica domanda: il numero tal dei tali (che in matematica non si chiama così, ma piuttosto x, o n, o…) numero è pari o dispari? Quando in matematica si è indecisi, conviene rifarsi alle definizioni. Che vuol dire che un numero è pari? Qualcuno, un po’ superficiale, vi direbbe, vuol dire divisibile per 2. Risposta senza senso se non si specifica in che insieme si vuol fare la divisione! Se mi metto nell’insieme dei numeri reali allora qualunque numero è divisibile per due! Se r è questo numero reale, bene diviso per due fa r/2, e questo ha perfettamente senso. Dunque no, non va bene dire divisibile per due, e basta. Il modo corretto di porsi il problema è dire: considero il numero naturale n, e dico che questo è pari se lo posso scrivere come 2xm, con m altro numero naturale. Dunque 6 è pari perché 6=2×3, mentre 5 non lo è perché non posso scrivere 5 come 2xm, con m naturale. Insomma divisibile per due sì, ma detto solo per numeri naturali, e in modo che il risultato sia ancora un numero naturale!
Quae cum ita sint, ne possiamo concludere che chiederci se 2,5, o 3/5, o pigreco, o radice(2) sono numeri pari è una domanda senza senso!
 Tra i non pochi argomenti appassionanti che la teoria dei giochi ti mette sotto il naso, questa è forse la storia più bella, più commovente, più illuminante che si possa immaginare. E’ la storia di una catena, nota come Catena 124, che riguarda le 60 persone che sono nella foto (in realtà sono 59, una non ha desiderato palesarsi). Cerco di raccontare questa storia, che ho riletto proprio oggi perché domani questa foto concluderà un mio seminario alla Sapienza. Devo premettere un po’ di cose, ma diversamente dal solito sono sicuro che valga davvero la pena andare fino in fondo alla storia…
Tra i non pochi argomenti appassionanti che la teoria dei giochi ti mette sotto il naso, questa è forse la storia più bella, più commovente, più illuminante che si possa immaginare. E’ la storia di una catena, nota come Catena 124, che riguarda le 60 persone che sono nella foto (in realtà sono 59, una non ha desiderato palesarsi). Cerco di raccontare questa storia, che ho riletto proprio oggi perché domani questa foto concluderà un mio seminario alla Sapienza. Devo premettere un po’ di cose, ma diversamente dal solito sono sicuro che valga davvero la pena andare fino in fondo alla storia…
Le malattie renali sono una delle cause più frequenti di morte (la dodicesima in US, quasi tutti i dati che metto qui vengono da lì). Come si cura una malattia renale avanzata? Esistono due possibilità: la dialisi e il trapianto. La dialisi rimpiazza all’incirca il 10% della funzionalità renale, è faticosissima (mediamente 4 ore per tre volta la settimana) e anche molto molto costosa. Un alternativa efficace è il trapianto.
Il primo trapianto renale sperimentale venne eseguito nel 1902 su un cane. Nel 1950 fu realizzato un trapianto di rene su una donna uremica, collegandolo ai vasi del braccio; l’organo iniziò immediatamente a produrre urina e dopo due giorni fu rimosso, una volta che i reni nativi ebbero ripreso a funzionare. Nel 1954 Joseph Murray realizzò il primo trapianto renale (tra gemelli monozigoti, il donatore è morto a 79 anni, 56 dopo la donazione!), e per la prima volta l’organo venne alloggiato nella fossa iliaca. Per questo intervento, Murray ottenne nel 1990 il premio Nobel per la medicina. Il primo trapianto in Italia venne effettuato da Aldo De Maria nel 1966. La maggior parte dei trapianti che sono fatti utilizzano organi da donatori deceduti. Tuttavia questi non bastano, né basteranno mai, perché anche se aumentasse la coscienza civile che sta dietro l’idea di donare gli organi, la richiesta tende comunque ad aumentare più rapidamente dell’offerta.
Ma il rene ha una grande particolarità: nasciamo forniti di due reni, ma ne basterebbe uno solo! Tutte le statistiche indicano che la speranza di vita di chi ha un rene solo ben funzionante non è inferiore a chi ne ha due… è evidente che sorge allora l’idea che un rene potrebbe essere donato da un essere vivente.
Dunque, è possibile che chi ha bisogno di un rene abbia anche uno o più potenziali donatori. Tuttavia, esistono problemi di compatibilità. Il primo è dato dal gruppo sanguigno. Non entro nei dettagli, un giorno se qualcuno me li chiederà proverò a spiegarli brevemente, questo tipo di incompatibilità è semplice ma non l’unico. Esiste anche la tipizzazione HLA, una cosa complicata ma che più o meno significa che abbiamo 6 antigeni (tre presi dalla madre tre dal padre), ognuno dei quali può essere di vari tipi differenti. Se per caso i sei che il paziente ha coincidono con i sei del donatore, si è a cavallo, ma questo non succede praticamente mai. Si può per fortuna procedere lo stesso, anche se più coincidenze ci sono e meglio, statisticamente, andranno le cose, ma…ovviamente c’è un ma. Potrebbe succedere che il paziente non solo non abbia la stesso antigene (di un certo tipo) del donatore, ma abbia addirittura sviluppato anticorpi nei confronti dell’antigene del donatore: in tal caso il trapianto è destinato a fallire…questo punto è spinoso in quanto un malato in genere sviluppa molti anticorpi, perché è sottoposto a cure, trasfusioni ecc ecc. e per di più questi anticorpi mutano nel tempo, il che rende ancora più complicata la gestione della faccenda.
Insomma, un terzo delle persone che hanno almeno un donatore a disposizione purtroppo non può sfruttarlo, proprio per motivi di incompatibilità: il rene del donatore sarebbe rigettato.
Ecco che allora nasce l’idea: perché non scambiarsi i donatori?
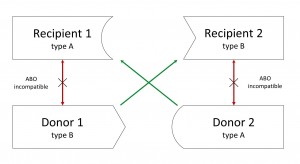 In figura c’è l’esempio di uno scambio diretto, il donatore del paziente 2 dona al paziente uno, e viceversa. Questo è un metodo semplice, il primo ad essere utilizzato, ma non è l’unico possibile. Ad esempio, sono possibili scambi indiretti, come nella figura seguente.
In figura c’è l’esempio di uno scambio diretto, il donatore del paziente 2 dona al paziente uno, e viceversa. Questo è un metodo semplice, il primo ad essere utilizzato, ma non è l’unico possibile. Ad esempio, sono possibili scambi indiretti, come nella figura seguente.
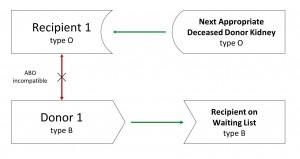
Qui il paziente 1, che ha un donatore incompatibile per gruppo sanguigno, riceve un rene da cadavere. Mette a disposizione comunque il suo donatore che dona alla lista d’attesa. Chiaro che sono possibili altre combinazioni, ad esempio la seguente.
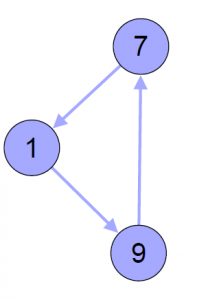
Qui il paziente 1 riceve il rene del donatore di 9, che prende il rene del donatore di 7, il quale prende il rene del donatore di 1
E veniamo allora alla storia, di cui voglio raccontare qualche frammento, che come dicevo comincia con un algoritmo e un altruista. L’algoritmo è stato inventato da un certo signor Hill. Il quale un giorno ha avuto la terribile notizia che l’influenza che stava angustiando la figlia in realtà nascondeva una nefropatia irrimediabile. La sua disponibilità a donare un rene alla figlia, pur con i gruppi sanguigni compatibili, si è scontrata con il fatto che la figlia aveva gli anticorpi verso un suo antigene. E’ per loro iniziato così un calvario, finito bene per fortuna, ma che ha convinto Mr Hill che si doveva e poteva fare di più. Messosi al lavoro, ha poco tempo dopo prodotto il National Kidney Registry, propagandandolo personalmente, e investendoci inizialmente 300.000 dollari a fondo perduto. Ma a volte la tenacia premia, e oggi il suo programma è il più utilizzato negli US, e quello che ha permesso che cominciasse questa storia che sto raccontando.
Ma la storia ha anche un altro genitore. Che in gergo si chiama buon samaritano.
Quando viene dato avvio a un ciclo-per esempio: il donatore di A dona il rene al paziente B, il donatore di B al paziente C, e il donatore di C chiude il ciclo donando al paziente A- i trapianti devono essere fatti in contemporanea. Infatti il donatore ha il (sacrosanto) diritto di ritirarsi anche un minuto prima dell’operazione, il che fa sì che vada evitata la situazione che uno che abbia già ricevuto il rene ritiri il suo donatore: questo significherebbe che il paziente che ha messo a disposizione il donatore rimane senza donatore e senza rene!
A meno che…a meno che la catena non inizi con un buon samaritano. Cioè con una persona che dona spontaneamente un rene alla comunità, senza avere un paziente collegato. Questo permette di fare trapianti differiti nel tempo, in quanto se qualcuno arresta la catena perché ritira il proprio donatore, rovina un programma di scambi ma non danneggia (almeno direttamente) nessuno.
Questa non è solo teoria… le 60 persone della foto inziale sono coinvolti in una delle più grandi, commoventi, spettacolari catene di scambio, in una delle più belle, toccanti manifestazioni del fatto che non siamo solo una specie assassina e violenta, ma che sappiamo anche fare cose meravigliose, e che la scienza è una conquista, di uomini certo, che hanno i loro difetti e le loro debolezze, che ci offre l’opportunità di fare cose splendide.
Il signore nella foto in alto a sinistra si chiama Rick Ruzzamenti: è lui il buon samaritano. Un tipo nulla di speciale, che nella vita non aveva combinato granché, e aveva passato i suoi guai…poi un giorno si è messo in testa l’idea di donare un rene, e alla fine c’è riuscito, nonostante le minacce della moglie di lasciarlo per sempre…e non dite che magari è per quello che ha insistito a farlo, oppure diciamolo, perché occorre sorridere anche nelle storie più drammatiche. L’ultimo signore si chiama Donald C. Jerry Jr, ed è la dimostrazione che nella vita non bisogna mai disperare, perché a meno di 50 anni la sua vita sembrava destinata all’angoscia della dialisi, e invece un giorno è stato il terminale di una catena di 30 persone che sono tornate sane grazie alla donazione di un rene da parte di un altro essere vivente: lui, senza donatore, selezionato tra 90.000 persone che erano nella sua situazione…una possibilità su 90.000…
Le foto di sopra sono la testimonianza di sessanta vite, ciascuna normalissima, quasi banale, ciascuna eroica, come ogni vita vissuta. C’è la storia di chi ha donato alla ex-moglie, da cui si era diviso con grandi rancori, ma che ha voluto aiutare perché, rimasto orfano da piccolo, non sopportava l’idea che sua figlia potesse perdere la madre. Ci sono due che si erano annusati da ragazzi, persi e ritrovati su facebook dopo che entrambi avevano divorziato. Vivendo lontani si vedevano poco, poi questa storia in cui uno ha ricevuto e l’altro ha donato li ha avvicinati per sempre. C’è un donatore di 62 anni, guarito da un precedente linfoma di Hodgkin, tanto per ricordarci che non abbiamo scuse a non mettere i nostri organi a disposizione della comunità quando a noi non serviranno più. E c’è una signora che ha aspettato 68 giorni tra il momento in cui il suo paziente di riferimento ha ricevuto il suo rene, e quello in cui è entrata in sala operatoria per donare il suo, 1632 ore di tempo per cambiare idea, ma non lo ha fatto.
17 ospedali, 11 stati diversi, persone che hanno sofferto, persone che hanno partecipato in maniera sostanziale alla riuscita della catena: dai chirurghi più bravi alle migliaia di persone che fanno andare avanti gli ospedali, che certo sono meno visibili del chirurgo in sala operatoria, ma non meno indispensabili a far muovere il tutto.
Ci sono state defezioni, momenti in cui si temeva che il processo si arrestasse precocemente: sono stati superati. Ed è stata scritta una storia splendida. Siamo una specie che fa la guerra, che picchia e ammazza le donne e i diversi: ce lo ricordano ossessivamente ogni giorno. Mi piacerebbe che qualche volta raccontassero queste storie, e altre magari meno spettacolari, ma che dimostrano che siamo anche capaci di collaborare, e di farlo in maniera straordinaria e con risultati straordinari
Pensavo stamattina a quanto siamo condizionati, nella valutazione di cose e persone, dalle nostre prime impressioni, nonostante i nostri sforzi di essere il più possibile corretti. E’ una cosa che probabilmente subiamo e abbiamo subito, ma anche che applichiamo costantemente agli altri, e non è detto che siamo sempre sottovalutati, anzi. Mi è venuto allora in mente la più curiosa esperienza di questo tipo che ho fatto da studente. Ho frequentato il primo corso di algebra al terz’anno, nonostante sia un corso per matricole, perché venivo da Ingegneria, dove il corso di algebra non esiste: però si fa un po’ di spazi vettoriali e applicazioni lineari in quello di geometria. Ora chiunque abbia fatto, magari al primo anno, un po’ di spazi vettoriali e algebra lineare, sa bene che la prima reazione è di panico assoluto: io raramente mi sono sentito più perduto di quando andavo alle lezioni del Prof. Gallarati che ci parlava di queste cose. Però sono un tipo testardo, anzi molto testardo, e quelle cose le volevo capire, e ci ho sudato su parecchio, fino a digerirle abbastanza bene. Poi c’è da dire che al primo anno vedere nel corso di algebra le definizioni di operazioni algebriche non è esattamente uno zuccherino da digerire: intanto arrivi che sei convinto che le operazioni siano quattro, e cominciano a spiegarti che no, quelle che conosci sono solo due, + e x, perché differenza e divisione non lo sono. Continuano poi a dirti che in realtà, oltre a quelle due, di operazioni ne possiamo definire un mucchio…insomma arrivi a 19 anni all’Università e ti sembra di essere finito in un mondo alieno. Ma se queste cose le vedi al terz’anno, beh allora la musica cambia. Per farla breve, quando arrivo a Matematica, dopo un mese perso di lezioni, al corso di algebra si stanno facendo proprio spazi vettoriali e operatori lineari…per me una manna, li sapevo già. Forse ho fatto qualche domanda o ho dato qualche risposta, fatto sta che un giorno l’assistente decide di chiamare me a fare gli esercizi alla lavagna; aveva l’abitudine di chiamare qualcuno, per vedere come venivano affrontati i problemi, dal momento che si impara molto più a vedere fare cose sbagliate e commentate che a vedere sempre tutto fatto bene. Io educatamente dico che preferisco di no, ma lui insiste. E’ andata a finire che in mezzora, nel silenzio più assoluto, ho risolto tutti gli esercizi che lui aveva preparato per due ore di attività…mi ha guardato risolverli in totale silenzio. Finita la lezione sono andato a parlargli: gli ho detto che ero del terzo anno, che venivo da Ingegneria, che quelle cose le avevo già studiate, che era quello il motivo per cui ero stato riluttante a andare alla lavagna… Il corso continua, e l’algebra insomma mi piace, e la capisco bene. Finalmente si arriva all’esame. Ci sono 20 esercizi (semplici) da svolgere, ognuno vale due punti, il tempo è di due ore, e ovviamente basta farne 15 giusti. Consegno dopo un’ora e me ne vado. Quando il professore ci distribuisce i compiti, dopo avermi fatto vedere il mio 38, che mi ha evitato anche la domanda per la lode, mi ha detto che ero davvero uno studente super. Io gli ho detto che ringraziavo, che certo capivo di aver fatto molto bene, ma insomma gli ho spiegato tutta la situazione, e lui mi ha detto che in effetti era vero che mi trovavo molto favorito rispetto agli altri…
L’anno dopo mi ritrovo lo stesso professore che ci fa algebra superiore (o qualcosa di simile). Siccome siamo in pochi, seguendo il metodo americano ci fa fare compiti a casa, che diventano parte integrante della nostra valutazione. Io come gli altri consegno il primo gruppo di esercizi, che dopo una settimana lui ci riporta corretti. A un certo punto mi guarda e mi dice: per favore, poi venga nel mio studio. Quando entro, mi prende letteralmente a male parole, alza la voce…io gli dico, va bene professore, ho sbagliato un esercizio, succede a me come agli altri. E lui che inveisce ancora di più: non si permetta, uno studente come lei capita una volta ogni trent’anni, e uno così non può fare errori simili, e io che gli racconto di nuovo la storia, ma non c’è verso, lui non mi ascolta. Mi minaccia ritorsioni (nel voto finale) se mi permetto di sbagliare di nuovo nei prossimi compiti…
L’ho sempre trovato una cosa ridicola. Quando mi sono laureato e sono diventato borsista, sono diventato amico dell’assistente più giovane di algebra. E lei mi ha raccontato che dopo la mia performance a esercitazione, l’altro assistente aveva cominciato a parlare di un fenomeno che andava a seguire le sue esercitazioni, e che in un ambiente così piccolo le voci girano…insomma mi ci sono voluti anni a convincerli che sì, forse bravino lo ero davvero, ma assolutamente in media, anzi perfino un po’ sotto… tra i bravini, s’intende. Comunque, in effetti alla fine sono riuscito benissimo a convincerli… anche perché sono passato al nemico, visto che mi sono dedicato all’analisi…